
関数不等式に付随する変分問題と偏微分方程式に関する研究。
無限次元の関数空間への理解から変分問題や偏微分方程式への応用に取り組む。

私の専門は、関数不等式と偏微分方程式という分野で、数学の中の解析学という学問分野になります。私はこれまでHardy不等式(i)のp=N(臨界)の場合として知られている臨界Hardy不等式(iv)に付随する臨界型変分問題を中心として、さまざまなHardy型不等式の改良や楕円型・放物型方程式への応用などの研究を行ってきました。
いくつか難しい用語が並びましたので、分かりにくいかもしれません。少し各用語を解説しましょう。専門用語や数式を使用するので、難しいかもしれませんが…。
臨界型変分問題について
変分問題とは、ある(エネルギー)汎関数の極値(特に最小値、最大値)を与える関数(しばしば最小化関数、最大化関数と呼ぶ)を求める問題で、高校数学で習う関数の極値を求める問題を、関数空間という無限次元空間上で考えたものです。ある現象が変分問題の解として与えられるとき、「変分原理に従う」と言いますが、光学におけるFermatの原理、古典力学における最小作用の原理、測地線の存在問題、等周問題、プラトー問題など、私たちの身のまわりの多くの現象が変分原理に従って起こっています。また変分問題は微分方程式と密接に関係しており、変分構造をもつような微分方程式の場合は、変分法が強力な手法として機能することが知られています。
最小化問題の達成可能性及び楕円型偏微分方程式の解の存在(以後、総称して「変分問題」と呼ぶ)を議論する際に中心的な道具となるのは、Sobolev空間の埋め込み定理であり、特に埋め込みのコンパクト性に関する定理が重要な役割を果たしています。具体的には、埋め込みがコンパクトであれば、最小化列もしくは近似解の列が適切に収束し、その収束先が最小化関数もしくは解となります。しかしながらSobolev空間は無限次元の空間であるために、対応する埋め込みのコンパクト性が欠如している場合は、近似解の列が適切に収束するかどうかは一般には分かりません。このようにコンパクト性が保障されていないような変分問題は通称「臨界型変分問題」と呼ばれ、取り扱いが非常に困難となるのはもちろんですが、複雑で興味深い現象が起こることが知られており、私を含めた多くの人々を魅了する問題の一つとして現在でも国内外で盛んに研究が行われています。

臨界型変分問題の例:Hardy不等式
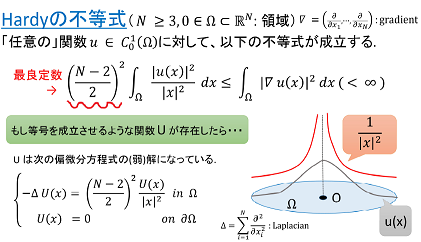
Hardy不等式は解析学の基礎的不等式のひとつです。上掲上段のHardy不等式を(i)とします。
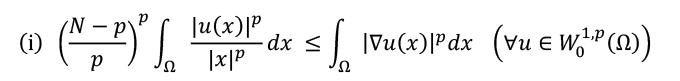

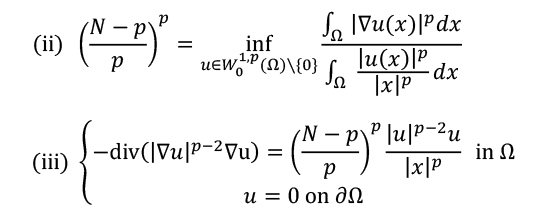
その下限を実現する最小化関数uが存在する(もしくは存在しない)場合に、「最小化問題は達成可能(もしくは達成不可能)」と云い、uは特に上掲(iii)の解となります。すなわち(iii)のような楕円型偏微分方程式の解の存在を示すためには、対応する最小化問題の達成可能性を示せばよいということになります。
前述の「Hardy不等式(i)のp=N(臨界)の場合として知られている臨界Hardy不等式(iv)に付随する臨界型変分問題」について
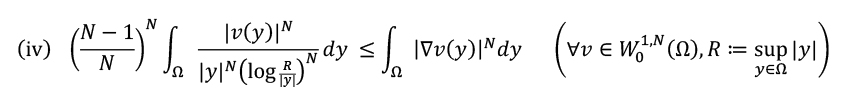
特に臨界Hardy不等式(iv)は、不等式の形や最良定数、ポテンシャル関数の特異性の構造が劣臨界Hardy不等式(i)と異なっているため、通常(i)とは別物として扱われますが、(i)と(iv)に付随する最小化問題に関する事実は、達成不可能となる理由までもが酷似していることを受け、別物と見なされていた劣臨界Hardy不等式(i)と臨界Hardy不等式(iv)は実は同一のものであるのではないかと予想し、実際にある変換を行うことで(i)と(iv)は最小化問題として同値となることを明示的に示しました。
また私はその研究をSobolev型不等式まで発展させ、2016年1月号の論説『数学』でも言及された一般化臨界Hardy不等式の最小化問題に関する未解決な問題について、解答を得ることに成功しました。
※これらの成果を発表した論文は、その独創性を高く評価され、2021年度日本数学会賞建部賢弘奨励賞を受賞しています。
高校数学とは全然違う「大学数学」。新たな道をつくるおもしろさ。
関数には滑らかで性質の良い関数や不連続な関数、特異性をもった関数など、いろいろなものがあります。それらを関数の滑らかさと特異性という尺度で測るものがSobolev空間です。Sobolev空間は変分問題を扱う舞台と考えてください。舞台、土台がしっかりしてないと、応用なども難しくなるので、研究を通して、その土台の整備をしているといった感じです。そして、関数の滑らかさと特異性が釣り合ってる状態を「臨界な状態」と言うのですが、現段階ではまだまだ分かっていないことが多いので、私はここを中心にずっと研究をしています。
私としては研究は、純粋な知的好奇心でやっているだけなので、分からないところを解明したいという想いに突き動かされているという状態です。そのため、研究に向かう姿勢として大切にしているのは、承認欲求を排除するということです。人の評価を気にせずに自分の思ったことや知的好奇心を大事にして、自由に研究することが肝心だと思います。特に数学の研究は考えても上手くいかないことも多く失敗ばかりでフラストレーションが溜まりやすいので、心身を健康に保つということも意識しています。それから、自分のペースで進めること、分からなくてもとりあえず手を動かすこと、試行錯誤することをポリシーとしています。
この道に進んだきっかけはというと、修士のときの学びでしょうか。もともとは高校の数学の先生になろうと数学科に入学し、教員免許を取得しました。その後、修士に上がるかどうかで悩んだときに、指導教員の先生から、修士に上がったら一種免許が専修免許になると教えてもらって、それならと思って修士に上がりました。修士では、じっくり数学の本を読んでみんなの前で発表するというようなことやるんですね。そこで本に書かれていた、すでに分かっている定理などの拡張、これをやったら、こう考えたらどうなる?という風に先生に言われて、自力で定理の拡張に取り組んだのが、研究者を目指したきっかけと言えます。それまでは勉強して理解するということをやってきたわけですが、勉強と研究は全然違っていて、研究というのはまったく道がないところに道をつくっていくというような、とても大変だけれども刺激的だと感じました。やっぱり研究っていいなと思って、その後、博士に進んでいまに至ります。
数理学研究室には教員が全部で7名います。私は変分問題を研究していますが、その他にも固有値問題や逆問題、微分方程式、力学系、数値計算など、数学のいろいろな分野を研究されている先生方がいらっしゃるので、自分の興味のある分野がもしあれば、あるいは理論的な話に興味があるという方は大歓迎ですので、是非、数理学研究室に来ていただけたらなと思います。
最後に、若い皆さんに対してひとこと。学生の頃というのは、すぐに答えが出ないのが嫌だったり、ちゃんとした答えを知りたがったりするような傾向があるように思うのですが、すぐに分からなくても、結果が出なくても、焦らずじっくり学んで欲しいと思います。頑張っても結果が出ないというのはよくあることです。それで不安になると思うのですが、若い頃に、結果にこだわらずにちゃんとじっくり学んできたかどうかが結構大事で、そうしたことが将来生きてくると思うんです。もう少し大きな目で、もうちょっと長いスパンでものを見てもらいたいと思います。どっしり構えると言うのでしょうか。私は30を越えてだいぶどっしりしてきたように思いますが、これがもう少し若い頃にあったらなぁといま思っているところです。


佐野 めぐみ 准教授
Megumi Sano
数理学研究室
2013年3月 大阪市立大学 理学部 卒業
2015年3月 大阪市立大学大学院 理学研究科 前期博士課程修了
2018年3月 大阪市立大学大学院 理学研究科 後期博士課程修了
博士号取得(理学) 大阪市立大学
2016年4月~2018年3月 日本学術振興会 特別研究員(DC2)(大阪市立大学)
2018年4月~2019年3月 日本学術振興会 特別研究員(PD)(東京工業大学)
2019年4月~2020年3月 広島大学大学院 工学研究科 テニュア・トラック准教授
2020年4月~ 広島大学学術院(先進理工系科学研究科) テニュア・トラック准教授


 Home
Home









