• A Hermitian interpolation for high-order Timoshenko elements matrix is developed.
• A distributed plasticity in frame elements using high-order functions is devised.
• The naïve p-adaptive procedure is enhanced with a machine-learning method.
• An outlier method is used as a more consistent procedure in the p-adaptive method.

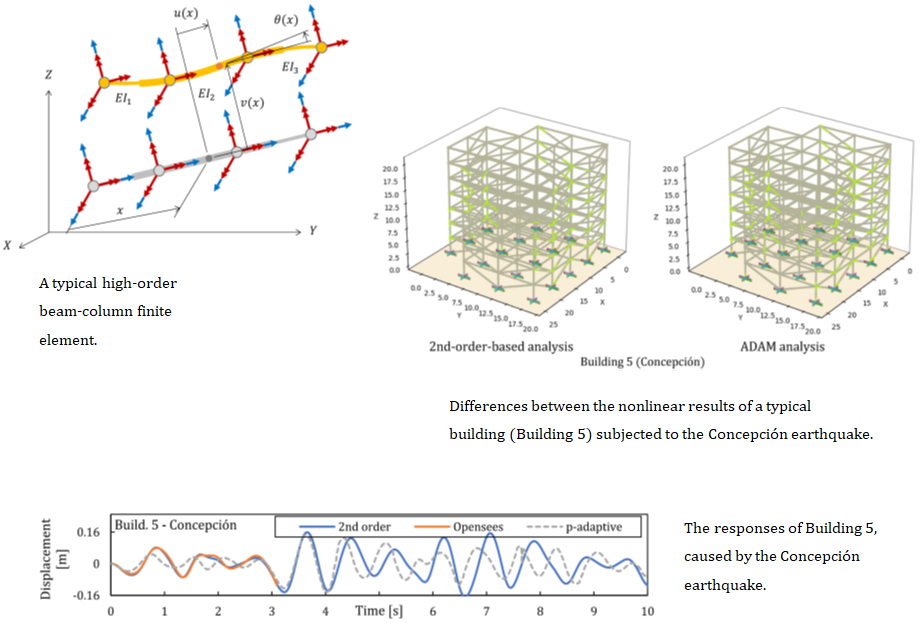
Structural analyses of buildings using beam-column finite elements are typically performed using procedures based on rotation polynomials truncated to the second order. This truncation will lead to inaccurate results that must be reduced. For this purpose, this study develops straightforward high-order Hermitian interpolation function matrices for Timoshenko elements. Moreover, a novel distributed plasticity hinge is devised. However, the structure complexity and the round-off error will increase with the interpolation function order. Nonetheless, a p-adaptive procedure can alleviate this problem. In contrast to other research, a technique for removing outliers for the maximum permissible error in the p-adaptive method is used to obtain results in a discrete space, rather than using integrals in the norm used, which is more consistent with the theory. Moreover, as with other studies, it has been observed that naïve p-adaptive processes diverge due to oscillations in the iterations. The proposed algorithm groups elements to be refined in different stages, employing the clustering function of the K-means method. Additionally, it is demonstrated that using fourth-order beam-column elements is also inefficient in elements that require refinement. After presenting the theoretical base, the importance of this investigation is demonstrated through examples of buildings of varying complexities.

Edgar David Mora Martinez, Naser Khaji*, 2024. An adaptive data-driven algorithm with machine learning for modeling high-order nonlinear beam-column finite elements. Journal of Building Engineering, 98, 111296. 
https://doi.org/10.1016/j.jobe.2024.111296