大学院先進理工系科学研究科 教授 中野 浩嗣
Tel:082-424-5363 FAX:082-424-5363
E-mail:nakano*hiroshima-u.ac.jp
(注: *は半角@に置き換えてください)
本研究成果のポイント
- 組合せ最適化問題をQUBO問題に変換し、解探索を行うためのC++プログラミング用ツール「QUBO++」を、非商用かつ評価・研究目的に限り無償で公開します。
- QUBO++には、QUBO問題の解探索をマルチスレッドで並列に行う2つのソルバー「Easy Solver」と「Exhaustive Solver」がバンドルされています。
- また、QUBO++は数理最適化ソルバー「Gurobi Optimizer」およびGPUを用いたソルバー「ABS2」を呼び出すためのAPIも備えています。
- QUBO++を使用することで、さまざまな組合せ最適化問題をQUBO問題に変換し、解探索を行うプログラムの開発をシームレスに行うことが可能になります。
概要
広島大学大学院先進理工系科学研究科の中野浩嗣教授らの研究チームは、株式会社NTTデータグループと共同で、QUBO(Quadratic Unconstrained Binary Optimization)問題を解くためのツールの開発に取り組んできました。多くの組合せ最適化問題はQUBO問題に変換することが可能であり、QUBOソルバーを使用してその解を求めることができます。しかし、この変換を行うプログラムの開発は容易ではなく、大規模な組合せ最適化問題においては変換処理に膨大な時間を要することが課題となっています。
今回公開するQUBO++は、組合せ最適化問題をQUBO問題に変換するためのC++プログラム(*1)を開発するためのツールです。これまでPythonベース(*2)のさまざまなツールが提供されていましたが、Pythonの処理系は動作速度が遅いため、複雑な処理を含む場合には変換処理に非常に多くの時間を必要とすることがありました。一方、QUBO++はC++ベースで実装されており、内部でマルチスレッドによる並列処理(*3)をおこなっているため、極めて高速な変換処理を実現しています。
また、QUBO++には、生成したQUBO問題を解くための簡易ソルバーとして、「Easy Solver」と「Exhaustive Solver」がバンドルされています。Easy Solverは、同研究グループが開発した解探索アルゴリズムPositive Min(発表論文[1])をマルチスレッド環境向けに実装したもので、単純ながら比較的高い解探索能力を備えています。一方、Exhaustive Solverは全解探索を最適コストで並列に実行する小規模QUBO問題用のソルバー(発表論文[2])であり、全ての最適解を列挙できるため、QUBO++で設計した変換ツールのデバッグにも活用できます。
さらに、同研究グループが開発したGPU(*4)を用いた高性能QUBOソルバーABS2(発表論文[3]、広島大学ニュースリリース[4])や、Gurobi Optimizer(*5)をQUBO++から直接呼び出すことが可能です。これにより、組合せ最適化問題を解くためのシームレスなプログラム設計が実現できます。さらに、Easy Solver、ABS2、Gurobi Optimizerを同時実行し、最適解を共有しながら高速に解を求める仕組みも提供されています。
なお、QUBO++は非商用かつ評価・研究目的に限り、無償で利用可能です。
背景
組合せ最適化問題は、物流の効率化、エネルギー消費の最小化、スケジューリングの最適化など、現代社会の幅広い課題を解決する鍵となる問題です。その解決は社会的コストの削減や持続可能な社会の実現に直結するため、極めて重要とされています。しかし、各課題に特化した専用ソルバーの開発には、高度な専門知識と膨大なコストが必要であり、大きな障壁となっています。
一方、多くの組合せ最適化問題がQUBO問題に変換可能であることが知られており、この性質を活用することで効率的な解決が可能になります。具体的には、解きたい組合せ最適化問題をQUBO問題に変換し、QUBOソルバーで解を求め、その結果を元の問題の解として逆変換する方法です(図1参照)。このアプローチを取ることで、高性能なQUBOソルバーを利用すれば、変換処理と逆変換処理を開発するだけで、組合せ最適化問題に対する高精度な解を得ることができます。
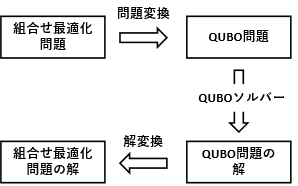
図1:QUBOソルバーを用いた組合せ最適化問題の解法
研究成果の内容
QUBO問題は、複数の2値変数に対する2次式を目的関数とし、その関数値を最小化するための0または1への割り当てを求める問題です。例えば、変数a、b、cの2次式f(a、 b、 c)=2ab-2ac-bc+a-bを目的関数とするQUBO問題を、QUBO++を用いて解くプログラムは次のように記述できます。
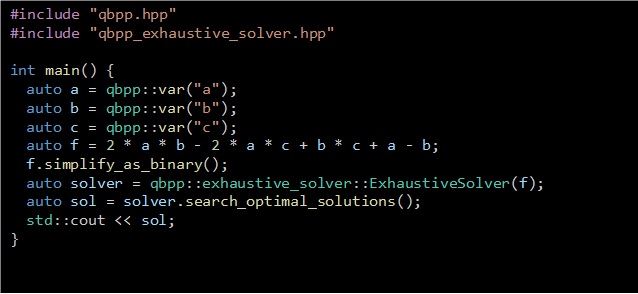
このプログラムを実行すると、次のような出力が得られます。この結果から、f(a、 b、 c)=-1となる2通りの最適解が得られていることがわかります。

QUBO++の実際のプログラム例として、平面グラフのノードを4色で塗り分ける最適化問題を取り上げます。平面グラフとは、平面上で辺が交差することなく描画できるグラフのことです。4色定理によれば、隣接する頂点が異なる色になるように、4色で塗り分けることが可能です。図2は、12頂点の平面グラフを4色で塗り分けた例を示しています。この4彩色問題をQUBO問題に変換する際には、大きさ12×4の変数の行列x=(xi,j)を用います。行列xの各行が1つのノードを塗るのに用いる色を表します。各行の4つの変数は、そのうち1つだけが1となり、1である場所がノードの色に対応します。
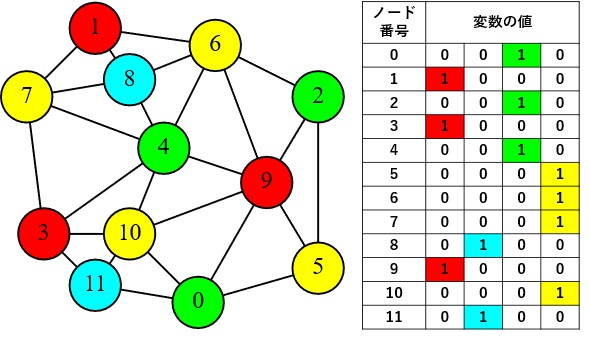
図2:平面グラフの4色での塗り分けと、変数の行列による塗り分けの表現
この問題をQUBO問題に変換するために、行列xに基づく二次式を作ります。行列xのi行目を長さ4のベクトルxi、その変数の合計をsum(xi)と表します。各ノードは1つの色で塗るので、sum(xi)=1でなければなりません。また、頂点iと頂点jが辺で接続している場合、異なる色でなければならないため、xiとxjの内積xi∙xjは0である必要があります。よって、平面グラフの4彩色問題は、次の2次式を用いてQUBO問題として表現できます。
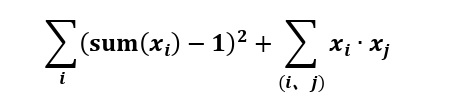
この2次式の値が最小値0となる行列xを求めることで、4彩色問題の解が得られます。QUBO++を用いると、この行列xの宣言と2次式の定義は次のように簡単に記述できます。

QUBO++を用いてQUBO問題の二次式を求め、Easy Solverを使用して解探索を行うと、ノード数が250の場合でも、図3に示すような正しい解を1秒以下で得ることができます。
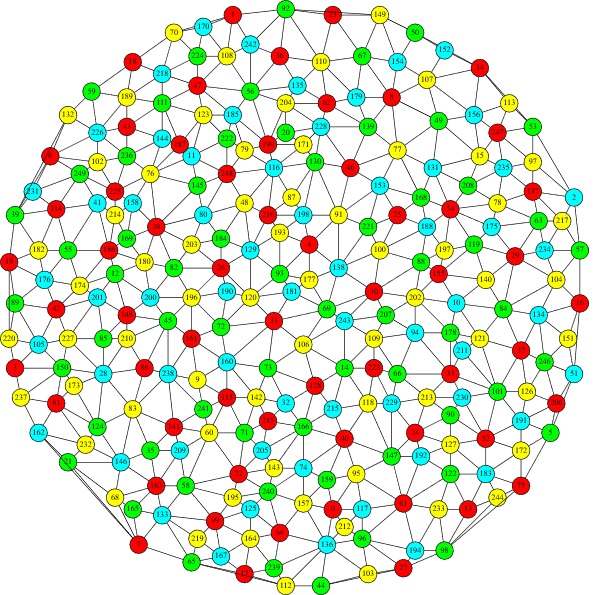
図3:ノード数250の平面グラフの4彩色
QUBO++は、Linux上でのマルチスレッドによる高速処理を可能にするよう設計されています。WindowsのWSLやMacOSでも動作が確認されており、IntelおよびARMのマルチコアCPUに対応しています。
また、QUBO++には、分割問題、ナップサック問題、ビンパッキング問題、N-Queens問題、整数計画問題、グラフ彩色問題、巡回セールスマン問題、素因数分解問題を解くサンプルプログラムが含まれています。これにより、利用者は多様な組合せ最適化問題に対応する実践的な手法を学ぶことができます。
今後の展開
QUBO++を用いて実社会に存在する組合せ最適化問題を解決する中で、ツール自体の改良を進めるとともに、高性能GPUソルバーであるABS2のさらなる性能向上を目指します。これにより、より広範な課題に対応できる柔軟性と高速性を備えたソリューションを提供し、社会全体における組合せ最適化の可能性を最大限に引き出すことを目指します
用語解説
*1 C++
コンピュータが効率よく動作するプログラムを作るためのプログラミング言語であり、高速処理が求められるオペレーティングシステムやゲーム開発などで広く使われています。また、C++はコンパイラによって最適化されるため、ライブラリだけでなく独自の処理を記述した場合でも、高いパフォーマンスが期待できます。
*2 Python
簡単に使えることを重視したプログラミング言語であり、データ分析、人工知能、ウェブ開発など、多くの分野で効率的に作業を進められることから人気があります。ライブラリを利用した定型処理では、内部でC++などによる高速処理を行なっているため高いパフォーマンスが期待できます。一方、ライブラリにない独自の処理をPythonで記述した場合、処理時間が非常に長くなるという欠点があります。
*3 マルチスレッドによる並列処理
一つのプログラムの中で複数の作業を同時に進める方法で、コンピュータの複数のコアを活用して処理時間を短縮することができます。
*4 GPU(Graphics Processing Unit)
グラフィクス処理のための専用集積回路であるが、汎用計算が可能なように拡張されており、多数のプロセッサコアを用いた並列処理を行うことができるため、現在の多くのスーパーコンピュータに搭載されています。
*5 Gurobi Optimizer
商用数理最適化ソルバーで、QUBO問題を含む幅広い最適化問題に対応しています。教育機関向けに無償のアカデミックライセンスも提供されています。
論文発表情報
- [1] High-throughput FPGA implementation for quadratic unconstrained binary optimization. Concurr. Comput. Pract. Exp. 35(14) (2023)
https://doi.org/10.1002/cpe.6565 - [2] A Work-Time Optimal Parallel Exhaustive Search Algorithm for the QUBO and the Ising model, with GPU implementation. IPDPS Workshops 2020: 557-566
https://doi.org/10.1109/IPDPSW50202.2020.00098 - [3] Diverse Adaptive Bulk Search: A Framework for Solving QUBO Problems on Multiple GPUs. IPDPS Workshops 2023: 314-325
https://doi.org/10.1109/IPDPSW59300.2023.00060 - [4] ABS2 QUBOソルバーのGPUエンジンを無償提供します~組合せ最適化問題を解くためのC++ APIの公開~、2024年1月1日
https://www.hiroshima-u.ac.jp/news/81193
詳細情報
QUBO++ツールとABS2 QUBO Solverの詳細情報: https://abs2.cs.hiroshima-u.ac.jp/

 Home
Home





