本研究成果のポイント
〇絡み目の絡み目ホモトピー類の分類を4,5成分絡み目に対して明示的に与えた。
〇4,5成分絡み目について、2つの絡み目が絡み目ホモトピー類として同じかどうかを判定するHabegger-Linアルゴリズムを実行可能にした。
〇絡み目の絡み目ホモトピーに対する不変量の構成を可能にする表を作成した。
○絡み目ホモトピー類の同値関係の生成元の個数に関する予想を立てた。
概 要
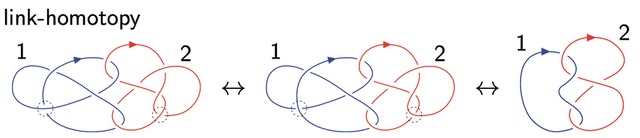
絡み目の分類や判定はトポロジーの一分野である結び目理論における古典的な問題である。絡み目とは3次元空間内のいくつかの紐であり、紐を手で連続的に動かして得られる紐も、同じ形の絡み目とみなす。本研究は、絡み目の分類や判定を、絡み目ホモトピーと呼ばれる通常より弱い関係性のもとで行ったものである。絡み目ホモトピーでは、絡み目は繋がっている紐同士であれば、互いにすり抜けさせても同じ絡み目と思うことができる。
HabeggerとLinにより、絡み目の絡み目ホモトピー類は、ストリング絡み目のある群作用により与えられていた。彼らによってストリング絡み目の絡み目ホモトピー類の分類とその標準形も与えられている。一方で、この作用の具体的な計算は与えられていなかった。本研究では、4,5成分絡み目(4,5本の紐からなる絡み目)に対する作用を計算することにより、絡み目の絡み目ホモトピー類の分類を明示的に与えた。この応用として、4,5成分絡み目に対して、2つの絡み目が同じ絡み目ホモトピー類かどうかを判定するHabegger-Linアルゴリズムを実行可能にし、その具体例を示した。また、これらの研究の過程において、一般の成分の絡み目に対する絡み目ホモトピー類の同値関係の生成元の個数の上限に関する予想を立てた。これらの研究は、従来のHabegger-Linの理論に、絡み目の局所変形理論を適用したことにより得られた成果である。
【論文情報】
Yuka Kotorii, Atsuhiko Mizusawa, Clasper Presentations of Habegger-Lin’s Action on String Links, EXPERIMENTAL MATHEMATICS, 2024, VOL. 00, NO. 0, 1–45
https://doi.org/10.1080/10586458.2024.2398150

 Home
Home





