By Hiroshima University Department of Public Relations
We chatted with Hiroshima University Professor Shoichi Fujimori about the beauty of zero mean curvature surfaces and the unexpected discoveries in this field.
Soap films are used in beautiful experiments to physically realize zero mean curvature surfaces. (Shoichi Fujimori)
Try to think about things of beauty and an equation is probably the last to pop in your head. One look at the zero mean curvature (ZMC) surfaces formula, however, and Professor Shoichi Fujimori was immediately captivated.
“First, we just felt the equation for ZMC surfaces is beautiful and wanted to know the surfaces,” Fujimori, who first saw the equation in his junior year as an undergraduate, said. He had since earned his doctorate in mathematics in 2006 and turned his fascination into a career in the field of differential geometry — dealing with the math of curves, surfaces, and manifolds.
A ZMC surface is a surface that takes up the least area with respect to its boundary. And to physically realize the different shapes assumed by ZMC surfaces, beautiful experiments that use soap films are conducted. But what charmed Fujimori the most are the unexpected discoveries in this field. ZMC surfaces have fascinated mathematicians, inspired innovators in designing the future of aerospace engineering, led architects to build superstrong structures using ultra-light materials, and showed how nature chooses its shape.
We chatted with Fujimori to learn more about the topic, the ZMC surface he developed, and the excitement over minimal surfaces’ global behavior.
HU Professor Shoichi Fujimori giving a lecture
Q: Can you tell us about the topic of your research?
My research topic is differential geometry in mathematics. There is a quantity on surfaces called “mean curvature.” In Euclidean space, a zero mean curvature (ZMC) surface is a surface at which each point of the surface has a neighborhood that is the surface of least area with respect to its boundary. Such soap films — not soap bubbles trapping air — are physical models of ZMC surfaces. ZMC surface theory is one of the classical subjects in differential geometry. In my research, we have developed a fundamental framework of ZMC surfaces in space-time, not in space. I have been studying this topic for about 10 years. The number of researchers who work on this topic is gradually increasing in Europe and Asia. In July 2020, there was an online workshop about ZMC surfaces in ICTS, India. I gave three lectures there
Q: That sounds fascinating. What problem, in particular, are you trying to address?
ZMC surfaces satisfy a certain kind of 2nd order partial differential equation (PDE). 2nd order PDE is ubiquitous in physics and engineering, such as fluid dynamics and so on. Locally, there are three types of 2nd order PDE, that is, elliptic type, parabolic type, and hyperbolic type. And each type of PDE is widely investigated. However, globally, there are 2nd order PDE of mixed type, and this kind of PDE’s are not yet well-investigated. ZMC surfaces satisfy a 2nd order PDE of mixed type and we have given a new method to investigate this kind of PDE. We would like to apply this method to many other kinds of PDE.
Q: Can you share more about the ZMC surfaces framework you developed?
There was a local construction method for ZMC surfaces in space-time. But there is no guarantee that the surface can be extended globally. In other words, applying the above method, we can locally construct a ZMC surface, but when we extend the surface, the surface may have singularities. The singularity of a surface is a point where the surface is not smooth, something like a cusp. We then gave some conditions so that the surface can be extended globally, and constructed a lot of ZMC surfaces without singularities.
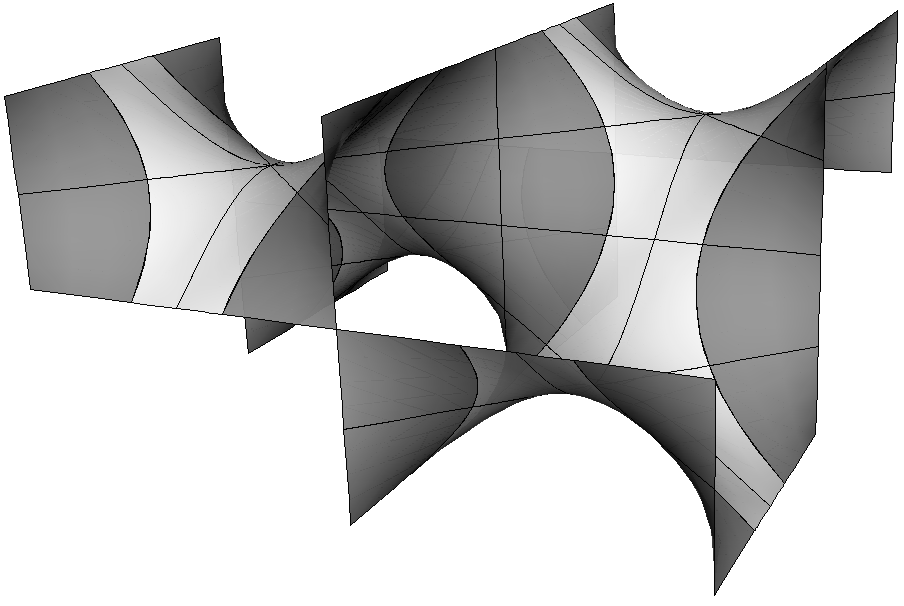
A ZMC surface in space-time.
Q: What is it that excites you about your topic?
First we just felt the equation for ZMC surfaces is beautiful and wanted to know the surfaces. Then later we realized that the theory we developed is closely related to some other theory such as fluid dynamics. What I want to say is go ahead the way that you believe, you would make an unexpected discovery.
Q: What's the next step in your research?
My dream is to find all of ZMC surfaces in space-time. But this is really my ultimate goal and I know we cannot solve this issue by ourselves. So I hope many people become interested in our research project and develop our work.
Q: You’ve said your dream is to find all ZMC surfaces in space-time. Can you share about the ones you’ve found so far?
We first found a triply periodic one, called Schwarz D-type ZMC surfaces. The original Schwarz D surface in space was found by H. A. Schwarz in the 19th century. "D" stands for Diamond because it has symmetry related to that of the diamond crystal structure. Then we found a lot more ZMC surfaces in space-time.
Q: Do you have a favorite ZMC surface?
My favorite ZMC surface in space-time is Schwarz D-type ZMC surfaces because these surfaces are the first example of ZMC surfaces in space-time with non-trivial topology. It is hard to explain what "topology" is, but intuitively "non-trivial topology" means "complicated shape."
(Research news authored by Mikas Matsuzawa)
Media Contact
Inquiries on the study
Professor Shoichi Fujimori
Graduate School of Advanced Science and Engineering
Tel: 082-424-7350
E-mail: fujimori*hiroshima-u.ac.jp
(Note: Please replace * with @)
Inquiries on the story
Hiroshima University Department of Public Relations
TEL: 082-424-3701
E-mail: koho * office.hiroshima-u.ac.jp
(Note: Please replace * with @)

 Home
Home

















