大学院先進理工系科学研究科 中野 浩嗣
Tel:082-424-5363 FAX:082-424-5363
E-mail:nakano*hiroshima-u.ac.jp
(注: *は半角@に置き換えてください)
発表のポイント
- 量子アニーラーで順列型組合せ最適化問題を解く場合に用いられる順列生成イジングモデルのサイズと要求分解能を大幅に削減する設計手法(dual-matrix domain-wall法)を開発しました。
- これまでよく用いられてきた単純なone-hot法によりn要素の順列生成を行うイジングモデルのサイズはn3-n2個であり、また要求分解能は2n-4でした。
- dual-matrix domain-wall法を用いると、サイズを6n2-8n、要求分解能を2に、それぞれ大幅に削減することができます。
- 300頂点の無向グラフに対する巡回セールスマン問題にdual-matrix domain-wall法を適用した場合、それを量子アニーラーで解くためのイジングモデルのサイズを従来のone-hot法より25分の1以下に削減することができました。
概要
広島大学大学院先進理工系科学研究科の中野浩嗣教授らの研究チームは、株式会社NTTデータグループと共同で、順列生成イジングモデルのサイズと要求分解能を大幅に削減する設計手法(dual-matrix domain-wall法)を開発しました。イジングモデル(*1)と呼ばれる複数のスピン変数の二次式は、量子アニーラー(*2)に埋め込み(*3)、量子焼きなまし(アニーリング)を行うことにより、イジングモデルの評価値をなるべく最小化するようなスピン変数へのスピン値の割り当てを求めることができます。量子アニーラーの規模と計算精度に制限があるため、イジングモデルのサイズと要求分解能(*4)をなるべく小さくすることが望まれています。
巡回セールスマン問題(*5)などの順列型組合わせ最適化問題を量子アニーラーで解くには、まず、順列を生成する順列生成イジングモデルを構成要素として含むイジングモデルに変換します。n要素0,1,…,n-1の順列を生成するイジングモデルではスピン変数からなるn×nの行列S=(si,j)を用い、one-hot表現(*6)で順列を表します。順列のi番目が要素jのときにsi,j=+1となります。図1は5×5行列による順列のone-hot表現の例で、巡回セールスマン問題の解の訪問順[3,1,0,2,4]を表しています。
スピン変数の行列S=(si,j )が、順列を表すone-hot表現を格納していることの必要十分条件は、行列Sのすべての行と列が+1を1個ずつ格納していることです。このような条件を満たす行列Sを最適解としてもつイジングモデルを順列生成イジングモデルと呼びます。幅広く用いられている従来のone-hot法では、 各行、各列の合計がすべて-(n-2)であることを利用する次の式を用いています。
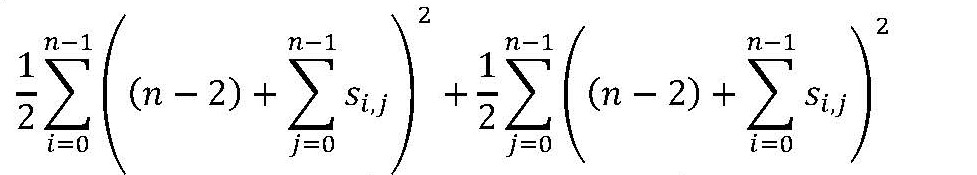
この数式を展開して得られる二次式が順列生成イジングモデルとなります.このイジングモデルのサイズはn3-n2であり、要求分解能は2n-4となります。
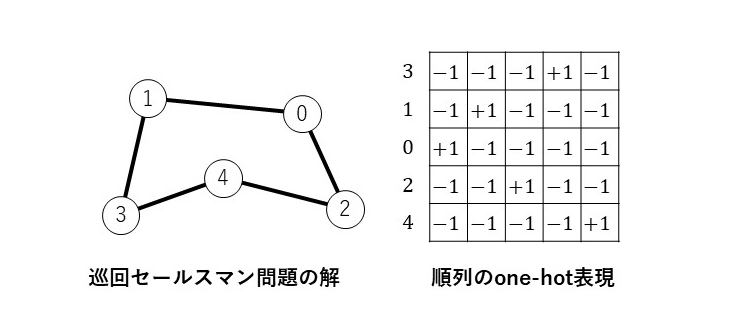
図1: 巡回セールスマン問題の解[3,1,0,2,4]とそれをone-hot表現で表す大きさ5✕5の行列
今回開発したdual-matrix domain-wall法によるイジングモデルでは、サイズを6n2-12n+4,要求分解能を2に、それぞれ大幅に削減しました。これにより、順列型組合わせ最適化問題をイジングモデルに変換し、量子アニーラーで解を求める場合に、より大きな問題を高い精度で取り扱うことができるようになります。
背景
社会における多くの問題は、制約の下で複数の選択肢から最適な組合せを見つける組合せ最適化問題として考えることができます。その中でも、順列型組合せ最適化問題は、n!通りある順列の中から最適なものを選ぶ問題で、巡回セールスマン問題や作業順の最適化など、多くのアプリケーションがあります。しかし、n!通りの膨大な組合せの中から最適なものを見つけるのは容易ではなく、膨大な計算時間を要します。
近年、量子効果を利用して組合せ最適化問題の解を求める量子アニーラーが注目されています。量子アニーラーを用いて組合せ最適化問題を解く手順は以下の通りです。まず、組合せ最適化問題を等価なイジングモデルに変換します。次に、変換されたイジングモデルを量子アニーラーに埋め込みます。このステップでは、量子アニーラーがイジングモデルの評価値を最小とする解を探索する準備を行います。その後、一定時間の量子焼きなまし(アニーリング)を繰り返し行うことにより、イジングモデルの評価値を最小化する解を探索します。最終的に、求めたイジングモデルの解を逆変換することで、もとの組合せ最適化問題の解が得られます。この手法により、従来の古典的なアルゴリズムでは扱いが難しかった複雑な組合せ最適化問題の解を、量子アニーラーが高速かつ効率的に求めることが期待されています。
順列型組合せ最適化問題を量子アニーラーで解くためには、n×nの行列S=(si,j ) を用いて、順列をone-hotで表現する方法が幅広く用いられています。しかし、各行各列の合計が-(n-2)となる条件を利用する従来のone-hot法では、順列生成イジングモデルのサイズがn3-n2と非常に多くなります。その結果、埋め込みに用いる量子アニーラーのセル数が膨大なものとなり、取り扱える順列型組合せ最適化問題のサイズ(nの値)が小さく制限されていました。また、要求分解能は2n-4であるため、nが大きくなると量子アニーラーの計算精度の限界を超え、最適解を得ることが困難になります。
整数を表すのにdomain-wall表現(*7)を用いれば、 one-hot表現に比べて、イジングモデルのサイズを削減できることが知られています。QUBOモデル(*8)でdomain-wall表現を順列生成に適用する方法が提案されています(Philippe Codognet: Domain-Wall / Unary Encoding in QUBO for Permutation Problems. Proc. of QCE 2022: 167-173).この方法(all-different domain-wall法)をイジングモデルに適用すると、サイズと要求分解能は、それぞれ1/2 n3-3/2 nとn-1に小さくすることができますが、約半分の削減にとどまっています。
研究成果の内容
今回開発したdual-matrix domain-wall法は、順列生成のためのイジングモデルであり、one-hot表現で順列を表すスピン変数のn×n行列S=(si,j)に加え、n×(n-1)行列A=(ai,j )と(n-1)×n行列B=(bi,j)を追加します。変数の個数が約3倍増加することになりますが、イジングモデルのサイズを6n2-8n個に、要求分解能を2に、それぞれ大幅に削減することができます。
図1の順列のone-hot表現において、各行がone-hot表現であるとみなした場合、得られる整数列 [3,1,0,2,4]は順列を表しています。一方、各列をone-hot表現とみなして得られる整数列[2,1,4,0,3]は逆順列(*9)を表しているとみなせます.dual-matrix domain-wall法では、行列Aの各行がdomain-wall表現で整数を表し、それを並べた整数列が順列を表します.同様に、行列Bの各列がdomain-wall表現で整数を表し、それを並べた整数列が逆順列を表します.それらが行列Sのone-hot表現による順列、逆順列とそれぞれ一致している場合に最適解になるように、イジングモデルを次のように設計します。
まず、次の3つの行列を導入します。
.∆S=(∆si,j):∆si,j=si,j+1(大きさn×n)
.∆A=(∆ai,j):∆ai,j=ai,j-1-ai,j(大きさn×(n-1))
.∆B=(∆bi,j):∆bi,j=bi-1,j-bi,j(大きさ(n-1)×n)
ただし、ai,-1とb-1,jは+1,ai,nとbn,jは-1とします.
これらの行列はスピン変数の行列でなく、スピン変数の行列S,A,Bから計算される行列です.次の条件を満たせば、スピン変数の行列Sにone-hot表現による順列が格納されます.
(1)行列Aの各行がdomain-wall表現
(2) 行列Bの各列がdomain-wall表現
(3) ∆Sと∆Aが等しい
(4) ∆Sと∆Bが等しい
これらの条件を全て満たす場合に評価値が最小になるよう、イジングモデルを設計します。
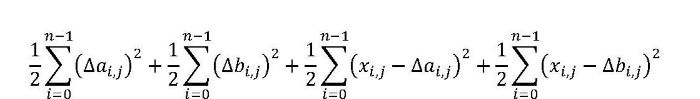
この式はsi,j,ai,j,bi,jを変数とする二次式に展開することができ、得られた二次式が順列生成イジングモデルとなります。4つの総和項が上の(1)から(4)の条件にそれぞれ対応します。4つの条件を満たすとき、4つの総和項のそれぞれが最小値2n,2n,0,0を取ります。したがって、このイジングモデルが最小値4nをとるとき、行列Sにone-hot表現による順列が格納されています.図2はスピン変数の行列S,A,Bが格納する値の例と、その場合の行列∆S,∆A,∆Bの各要素の値を示しています。(1)~(4)の条件をすべて満たしていることが確認できます。このイジングモデルの二次項の個数は6n2-8n、要求分解能は2となり、従来のone-hot法による順列生成イジングモデルより大幅な削減となっています。
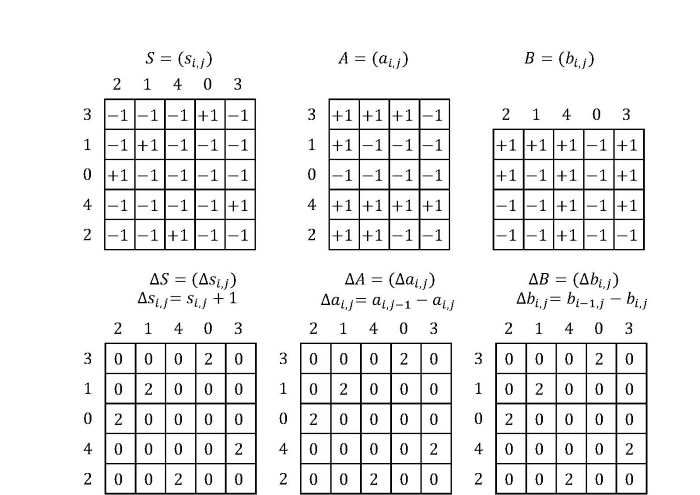
図2:Dual-matrix domain-wall法によるイジングモデルの最適解の例.この最適解は順列[3,1,0,4,2]とその逆順列[2,1,4,0,3]を表している。
順列型組合せ最適化問題には、例えば、巡回セールスマン問題、グラフ同型問題、二次割当問題などがあります。順列生成イジングモデルはこれらの問題に適用可能です。例えば、無向グラフの巡回セールスマン問題(*10)では図3の重み付き無向グラフが与えられたときに、すべての頂点を一度ずつ訪問する最短巡回を求めます。図3では、巡回順を表す順列[0,1,4,8,…,3]が最適解になります。図4のグラフは、このような接続関係が平面の重み付き無向グラフについて、巡回セールスマン問題を解くイジングモデルを生成したときのサイズを表しています。グラフの頂点数が多くなると、従来のone-hot法ではサイズが急激に増加します。all-different domain-wall法を用いることにより、サイズが約半分に節約できています。一方、dual-matrix domain-wall法は、頂点数の増加にともなうサイズの増加がこれら2つの方法に比べ極めて緩やかであり、無向グラフが頂点数300のときは、従来のone-hot法に比べて25分の1以下に削減できています。
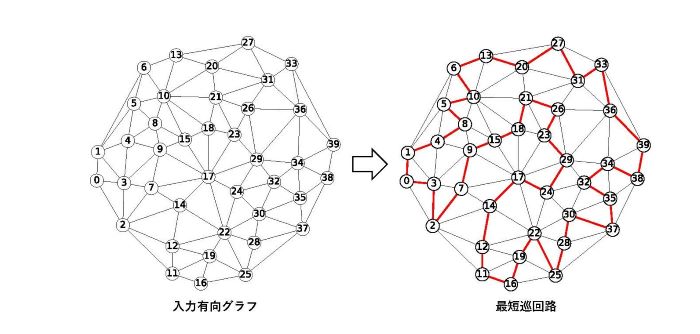
図3:40頂点の有向グラフと最短巡回路
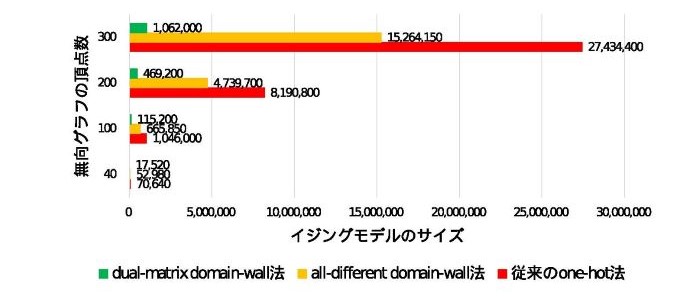
図4:無向グラフの巡回セールスマン問題を解くイジングモデルの二次項の個数
なお、dual-matrix domain-wall法の技術内容は特許出願済みです。また、論文プレプリントでは、部分順列生成(*11)へのdual-matrix domain-wall法の拡張や、二次割当問題、部分グラフ同型問題、マッチング問題などへ適用した場合の二次項の個数、最新の量子アニーラーD-Wave Advantageのペガサスグラフに順列生成イジングモデルを埋め込んだ場合に使用するセル数の評価を行っています。
今後の展開
順列型組合せ最適化問題は多くのアプリケーションがあるにもかかわらず、それを解くためのイジングモデルはサイズと要求分解能が大きくが大きいため、実際の量子アニーラーを用いて最適解を得るのは困難でした。今回開発したdual-matrix domain-wall法は、これらの課題を解決する大きなブレイクスルーと言えます。ただし、現時点での量子アニーラーはまだ規模が小さく、計算精度も十分ではないため、従来の古典計算機を用いた問題解法を凌駕するには、量子アニーラーの大規模化と高性能化が待たれます。一方、それまでの代替として、量子効果に基づかず、イジングモデルの解を求める疑似量子アニーラーの研究が盛んに行われています。我々の研究グループでもGPUを用いた疑似量子アニーラーABS2(https://abs2.cs.hiroshima-u.ac.jp/)を開発しており、dual-matrix domain-wall法を含めた様々な手法を用いて組合せ最適化問題の高速解法を探求していく予定です。
用語解説
*1 イジングモデルとグラフ表現
イジングモデルは、-1または+1の値をとる複数のスピン変数の二次式です.例えば、4変数s0,s1,s2,s3のイジングモデル
s0s1-2s0s2-s1s2+s1s3-2s2s3+s0-2s1+s2+3s3
は5つの二次項(-2s0s2など)と4つの一次項(3s3など)から構成さています。また変数を頂点、二次項を辺としてグラフで表すと図5のようになります。このイジングモデルはs0=s2=s3=-1,s1=+1のとき、最小値-12をとる最適解となります。また、二次項の個数、つまりグラフの辺の個数(この例の場合5)をイジングモデルのサイズと呼びます。
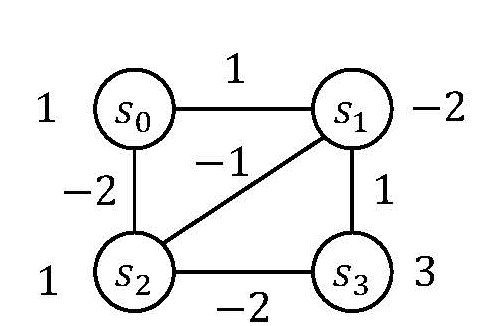
図5:イジングモデルのグラフ表現
*2 量子アニーラー
量子効果に基づいて、特定のグラフ形状をもつイジングモデルの解を求める量子コンピューターを「量子アニーラー」と呼びます。D-Wave Systems社の開発した量子アニーラーD-Wave 2000Qは、2048個のセルがキメラグラフの形状で接続されています。各セルをイジングモデルの変数とその一次項に対応付け、セル間の接続を二次項に対応付けるよう設定すると、そのキメラグラフの形状をもつイジングモデルの解を量子焼きなまし(アニーリング)により求めることができます。図6は128セルのキメラグラフを示しており、これを16倍の大きさ(縦横それぞれ4倍)に拡張したものが2048セルのキメラグラフです。
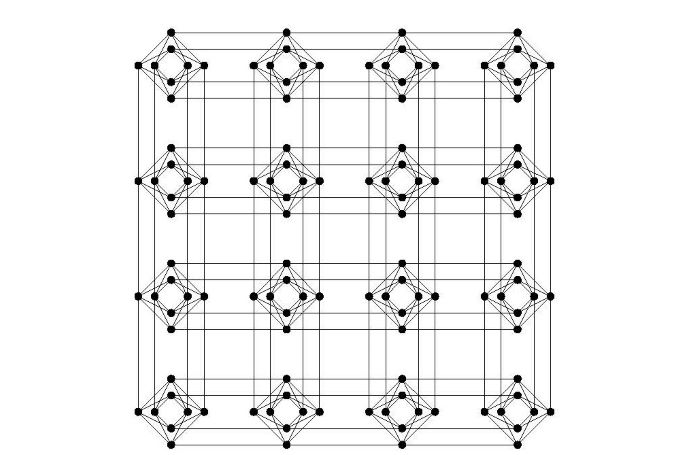
図6:128セルのキメラグラフ
*3 イジングモデルの量子アニーラーへの埋め込み
量子アニーラーD-Wave 2000Qでキメラグラフとは異なる形状のイジングモデルを扱う場合は、事前に埋め込みを行います。この埋め込みでは、イジングモデルの変数をキメラグラフのセルに対応付けます。対応付けは、イジングモデルの接続関係がキメラグラフ上で維持されるように定める必要があります。
図7は、17変数イジングモデルと33変数イジングモデルの128セルのキメラグラフへの量子アニーラーへの埋め込みをそれぞれ示しています。17変数イジングモデルは、変数のすべての組合せに二次項を持つため、密なイジングモデルとなっています。一方、33変数イジングモデルの各変数は最大で4つの二次項を構成しており、疎なイジングモデルです。変数とセルの対応は接続関係を維持するように定める必要があるため、イジングモデルの各変数がキメラグラフの複数のセルに割り当てられています。疎なイジングモデルの方が変数の個数は多いにもかかわらず、サイズ(二次項の個数)が小さいため、使用するセルの数はかなり少なくなっています。したがって、変数の個数よりもサイズを削減することが、埋め込みに必要となる量子アニーラーのセルの個数の節約につながります。
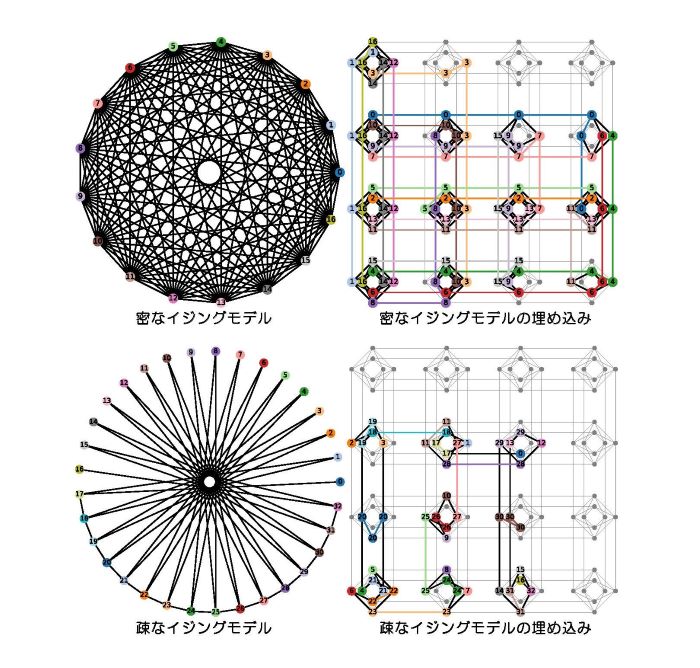
図7:密な17変数イジングモデル(二次項の個数:136)と疎な33変数イジングモデル(二次項の個数:51)の128頂点キメラグラフ(右側)への埋め込み。例えば、疎なイジングモデルの変数31は、右側のキメラグラフでは2つのセルに割り当てられています.イジングモデルでは変数31は変数14,15,30,32と接続していますが、対応付けられたセルにおいてもこれらの接続が維持されています。
*4 量子アニーラーの計算精度とイジングモデルの要求分解能
整数係数に限定したイジングモデルにおいて、係数の最大絶対値を要求分解能と呼びます。この値が大きいほど、量子アニーラーに高い計算精度を要求することになります。それは次のような係数圧縮が行われるためです。
実際の量子アニーラーで扱うイジングモデルの係数は例えば範囲が-1.0~+1.0というように範囲指定された実数値を設定できます。しかし、イジングモデルが量子アニーラーに要求する計算精度を正確に評価するために、あえてイジングモデルの各項の係数を整数に限定することが行われます。そのようなイジングモデルを量子アニーラーで扱う際には、整数係数の最大絶対値(要求分解能)で各係数を除する前処理を行います。これにより、係数を-1.0~+1.0の範囲に圧縮して、量子アニーラーで扱えるようにします。例えば、上記のイジングモデルの場合、要求分解能である3で除して次のようになります:
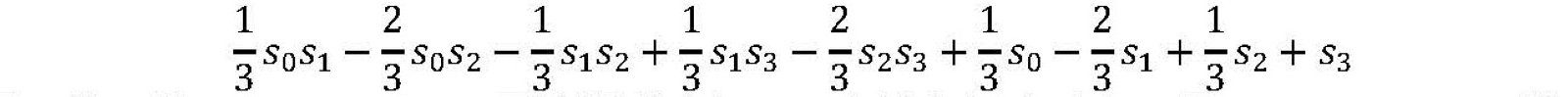
同じ値で除しているので、最適解が変わることはありません。量子アニーラーの計算精度は限られているため、除する整数が大きくなると、絶対値の小さい係数や差の小さい2つの係数が現れることがあります。そのような小さい係数や係数の差を正しく取り扱うことができなくなるため、計算精度が限られた量子アニーラーでは最適解を得るのが困難になります。以上より、イジングモデルの係数の最大絶対値、つまり、要求分解能は小さい方が望ましいと言えます。現在の量子アニーラーの計算精度は5~6ビット程度と言われており、要求分解能は25=32程度が限界です。
*5 巡回セールスマン問題
複数の都市が入力として与えられて、それらをすべて一度ずつ巡る訪問順で総巡回路長が最短のものを求める組合せ最適化問題。訪問順は都市の順列なので、順列型組合せ最適化問題です。
*6 スピン値によるone-hot表現
0からn-1の整数を表すのに、n個のスピン値を用い、k番目が+1,他が-1のとき、整数kを表すとみなします。ここで、先頭は0番目であり、例えば、 [-1,-1,-1,+1,-1]は3を表します。n個のスピン変数s0,s1,…,sn-1がone-hot表現であるスピン値を格納するためのイジングモデルは、合計が(-1)×(n-1)+(+1)×1=-(n-2)となることを利用して次の二次式で得られます。
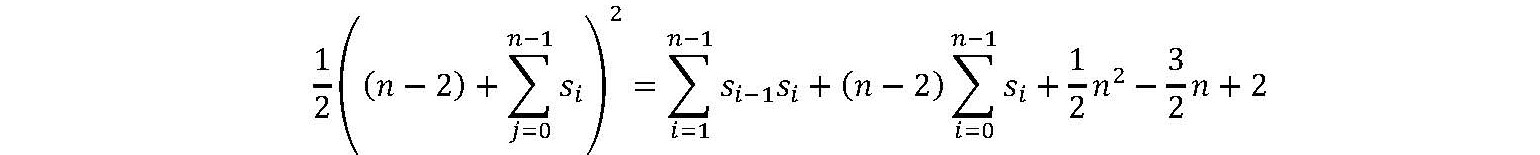
n個のスピン変数がone-hot表現のとき、この式の評価値は最小値0となります.このイジングモデルのサイズは1/2 n2-1/2 nであり、要求分解能はn-2となります.また、図1の行列のように、n×nの行列の各行がone-hot表現で整数を表し、それらの整数が異なる場合、得られる整数列は順列となります.これを順列のone-hot表現と呼びます.
*7 スピン値によるdomain-wall表現
0からn-1の整数を表すのに、n-1個のスピン値を用い、先頭からk番目までが+1、残りが-1のとき、整数kを表すとみなします。ここで、先頭は0番目であり、例えば、 [+1,+1,+1,-1]は3を表します。n-1個のスピン変数s0,s1,…,sn-2がdomain-wall表現であるスピン値を格納するためのイジングモデルは、+1と-1が隣り合っているところが一箇所であることを利用して次の二次式で得られます。
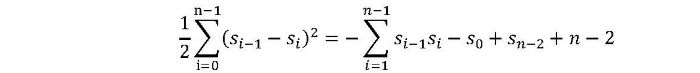
ここで、s-1=+1,sn-1=-1として左辺を展開しています。n-1個のスピン変数がdomain-wall表現のとき、si-1-si=2となるのは一箇所で、それ以外は0となります。よって、この式の評価値はdomain-wall表現のときに、最小値4となります。このイジングモデルのサイズはn-2であり、要求分解能は1となり、one-hot表現に比べて大幅に小さくなります。
*8 QUBOモデル
QUBO(Quadratic Unconstrained Binary Optimization)は、 0または1の値をとる複数のバイナリ変数の二次式です。イジングモデルとは変数がスピン値かバイナリ値を取る点のみ異なります。QUBOモデルとイジングモデルは、そのグラフ形状(接続関係)を変えることなく等価に変換可能であり、また、変換によりサイズは変わりません。
*9 順列と逆順列
n要素の2つの順列P=[p(0),p(1),…,p(n-1)]とQ=[q(0),q(1),…,q(n-1)]が全てのiについてq(p(i))=i成り立つ時、つまり、逆関数の関係になっている時、PとQは互いに逆順列です。
*10 無向グラフの巡回セールスマン問題を解くためのイジングモデル
頂点数nの無向グラフの頂点集合を0,1,…,n-1とし,辺集合をE,辺(u,v)∈Eの長さをwu,vとします。また、辺の長さの最大値より十分大きい値Mを決めます。one-hot表現による順列を格納するスピン変数の行列S=(si,j)としたとき、次の式により、順列が定める訪問順による巡回路長を評価することができます。
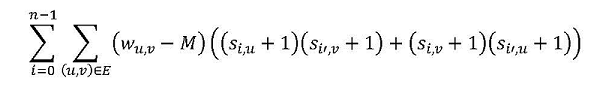
ただし、i'=(i+1)mod nとします。i番目に訪問する頂点がuであり、その次のi'番目に訪問する頂点がvである場合にsi,u=si',v=+1となります。よって、(si,u+1)(si',v+1)=4が成り立ち、この式の評価値は、one-hot行列が表す訪問巡の巡回路長の4倍から4Mをマイナスした値となります。式の中で-Mは、辺がない場合の係数を0として、辺がある場合にその長さに応じて負の値とするためです。これにより辺のない訪問巡を選ばなくなります。この式を展開して得られるイジングモデルと順列を表す行列S=(si,j)を生成するイジングモデルをあわせることにより、最短巡回路を求めるためのイジングモデルを得ることができます。
*11 部分順列
n個の要素からm個(m<n)の要素を重複なく選んで並べる順列。例えば、n=5,m=3のとき、0,1,2,3,4から3個選んで並べた[3,0,1]は部分順列です。
発表情報
出願特許:特願2023-125848 「モデル生成装置、モデル生成方法、順列生成システム、およびプログラム」
論文プレプリント:「Dual-Matrix Domain-Wall: A Novel Technique for Generating Permutations by QUBO and Ising Models with Quadratic Sizes」https://doi.org/10.48550/arXiv.2308.01024
※Technologies に招待論文として採択決定・掲載予定
特別講演(Plenary Talk):「Reducing Ising Model Sizes for Solving Permutation-Based CombinatorialOptimization through Dual-Matrix Domain-Wall Encoding」The 7th ZIB – IMI – ISM – NUS – RIKEN – MODAL Workshop on Future Algorithms and Applications, 2023年9月27日-10月1日(https://optimizationworkshop2023.zib.de/)

 Home
Home